Добро пожаловать на пятый урок! Чтобы рисовать на графическом планшете нам необходимо научиться создавать трёхмерные, объемные рисунки. В этом уроке мы разберем самые основы перспективы и простые примеры. Поэтому если вы хотите подробнее углубится в тему перспективы, вам будут полезны следующие уроки:
Курс рисования на графическом планшете. Урок №8 - Линейная перспектива
Курс рисования на графическом планшете. Урок №9 - Перспектива окружности
Итак, Почему же некоторые изображения выглядят трехмерными. Все зависит от ракурса - вид сбоку более плоский, чем вид в три четверти. Следовательно, чертеж выглядит двухмерным, так как вы видите только одно или два измерения. Чтобы он выглядел трехмерным, вам нужно показать все три измерения.


Можно легко представить себе полную трехмерную форму объекта (или, скорее, другие двухмерные виды) просто наблюдая, как объект изменяется во время вращения.
Первое - когда вы вращаете объект вокруг одного измерения (например красного - как на рисунке), оно остается неизменным. Два других (синий и зеленый) меняют длину и положение.

Во время вращения одно измерение, как будто превращается в другое:

Вы видите, как линии переходят друг в друга? Только красный остается неизменным, потому что это ось вращения.
Чтобы начать такой рисунок, нужно всего три линии:

Но что, если вы хотите увидеть и третью сторону? Мы можем повернуть куб слегка вниз, чтобы показать верхушку и снова начать вращать.

Снова одна плоскость постепенно сменяется другой. Только теперь они меняют не только длинну - это влияет и на угол между сторонами.

Чем больше вы видите сторону, тем более тупой угол - и тем короче и острее другая сторона.

Попробуем нарисовать такой куб:

Вы рисуете не куб - вы рисуете линии определенной длинны и углы, которые наш мозг воспринимает как повернутый куб.
ПРОЕКЦИЯ ИЗ 2D В 3D
Рисовать плоские предметы в 2D проще всего, есть только высота и длинна. Но когда мы рисуем сложные предметы в перспективе, нам не только нужно думать о углах и трех сторонах одновременно, появляется ещё разница ширины частей, как на примере с игрушечным котёнком.

Для рисунка игрушки сначала можно максимально упростить формы. Более подробно мы это разберем в следующем Уроке № 6 - Думайте формами.

Чтобы создать проекцию, нам достаточно вида сбоку. Мы спроецируем его на обе стороны прямоугольного контейнера, который соответствует габаритам игрушки, как показано ниже:

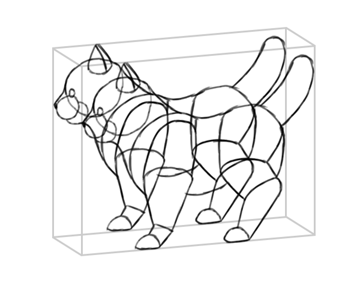
Сложность в том, что не все части игрушки одной ширины.

Поэтому нам придется сократить растояния некоторых частей: мордочки, хвостика, ушек ...


Мы как будто сшиваем две половинки мягкой игрушки вместе. Как видите, расстояние носика и ротика нам придется свести к нулю:


Готово! Это не лучший способ рисования в перспективе, но очень простой и наглядный пример концепции сторон в 3D проекции.

ПОНИМАНИЕ КОНЦЕПЦИИ СТОРОН.
Когда мы рисуем животных, геометричные прямые линии, углы и градусы практически отсутствуют. Но сама концепция сторон остается.


ОСНОВНЫЕ СТОРОНЫ.
В любом объекте можно найти шесть основных сторон, даже если он имеет очень сложные поверхности и гладкие края:
- Передняя
- Задняя
- Верхняя
- Нижняя
- Правый бок
- Левый бок

Давайте рассмотрим их на примере морской свинки:

Но мы не можем видеть больше трех сторон одновременно.


В отличии от прямоугольников, морская свинка имеет окружности (эллиспы). Формы окружностей меняются в зависимости от ракурса и положения линии горизонта (уровень глаз).
- A: Это уровень глаз, где окружность похожа на линию.
- B: Чем выше цилиндр, тем шире форма окружности.
- C: Чем ниже цилиндр, тем также шире окружность.

То же самое относится к боковым окружностям, если цилиндр расположен горизонтально:

А - не только обозначает линию горизонта но и точку схода, поэтому линии окружности центральной свинки абсолютно прямые.

По мере отдаления от точки схода и линии горизонта (уровень глаз), окружности становятся объемнее.

Более подробно этому будет посвящен следующий Урок №9 - Перспектива окружности
ОСНОВА ПЕРСПЕКТИВЫ И АКСОНОМЕТРИЯ
На уроках геометрии, нас учат чертить фигуры, состоящие из трех координат: ширину, высоту и глубину, но не так, как мы видим вещи на самом деле. Перспектива в данном случае обычно игнорируется, просто сравните эти два куба: один из них легко начертить, но другой выглядит более реалистичным.

В чем разница? Все дело в углах и прямых линиях. Передняя плоскость первого куба выглядит как квадрат (прямые углы, равные стороны) такое возможно только если вы смотрите на куб напрямую. Когда куб вращают, он теряет свои прямые углы, одна сторона становится короче, другая становится шире — чтобы в итоге снова достичь угла 90 градусов (прямой угол, равные стороны), как показано ниже:

Другими словами — две грани одного и того же объекта не могут быть видны полностью одновременно.

Перспективе подчиняются не только прямоугольники с прямыми линиями и углами, но и овальные, угольные и многоугольные фигуры. Все они имеют оси: ширины, высоты и глубины, которые определяют вид и угол наклона трехмерной фигуры.
РИСУНОК КУБИКА
Попробуем нарисовать кубик, используя три оси координат.

Шаг 1. Представьте себе одну горизонтальную сторону квадрата и поверните ее — чем больше поворот, тем короче должна быть линия.

Шаг 2. Перекрестите ее посередине с другой осью. Хотя она такой же длины, как первая, перспектива изменит ее — чем длиннее первая линия, тем короче вторая. Также можно ориентироваться на угол наклона — чем ближе к горизонтальному положению, тем длиннее линия, и тем короче другая.

Шаг 3. Добавьте копии линии по обеим концам осей, чтобы получился квадратный контур.

Шаг 4. Это были всего две оси: ширина и глубина. Давайте добавим ещё третью, по высоте равную предыдущим, но без влияния перспективы.

Шаг 5. Продублируйте оси ширины, глубины и квадратный контур, на верху оси высоты.

Шаг 6. Осталось соединить углы квадратных контуров и наш кубик готов!

РИСУНОК ПАРАЛЕЛЕПИПЕДА
Проделаем тоже самое с паралелепипедом.
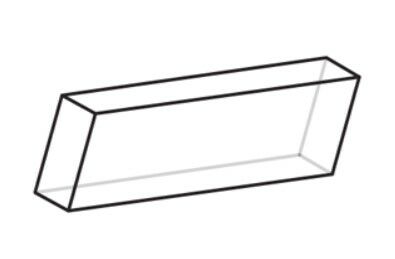
В отличии от кубика, вертикальная ось будет слегка наклонена, что повлияет на все вертикальные углы паралелепипеда.



Начиная с этого этапа, можно было бы превратить фигуру в трапецию или в призму. Всё зависимости от угла наклона и направления вертикальной оси.



РИСУНОК МНОГОУГОЛЬНИКА
Как вы, вероятно, догадываетесь, многоугольник имеет три горизонтальные оси и ни одного прямого угла между ними. Что делает его довольно сложным в построении.

Шаг 1. Нарисуйте первую ось любой длинны удобным для вас способом.

Шаг 2. Перекрестите ее другой осью той же длины. Они обе должны выглядеть как наклоненная «X».

Шаг 3. Пересеките их третьей осью той же длины, но сокращенную под влиянием перспективы.

Шаг 4. Соедините оси, образовав многоугольник. В результате, любые две противоположные линии, должны получится паралельными друг другу.

Шаг 5. Теперь добавьте четвертую ось высоты многоугольника.

Шаг 6. На этот раз, чтобы скопировать нижний многоугольник, сначала скопируйте оси.

Шаг 7. Соедините верхние концы осей с нижними. Должны получится прямые вертикальные линии.
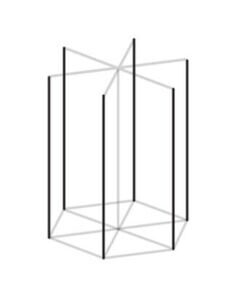
Шаг 8. Теперь соедините верхние концы осей между собой. Получится верхний контур и многоугольник готов!

ВРАЩЕНИЕ СТОРОН
Вы можете знать, как рисовать отдельные 3D фигуры повернутые к нам в три четверти, но иногда вращение влияет на общую систему координат и усложняет работу.
Допустим, вы хотите нарисовать:
1. Открытую дверь;
2. Открытую коробку;
3. Открытую челюсть.

Для начала найдите ось вращения (как правило это одна из сторон объекта), а также выберите точку траектории вращения.

Ось вращения выделена пурпурным.
Теперь нарисуем траекторию вращения, она должна иметь форму круга, но в перспективе это будет эллипс.

Нарисуйте любой угол, под которым вы хотите открыть дверь (коробку или челюсть).

Так как одна сторона двери у нас уже есть, другая сторона будет повторять тот же угол.

Осталось только добавить толщину, она будет следовать направлению оси вращения.
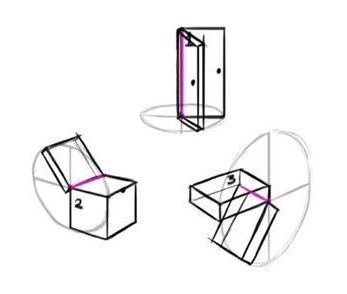
Не забывайте про аксонометрию – вы либо показываете прямой угол и одну / две стороны, либо три стороны без прямого угла. Не говоря уже о сокращении сторон, которое мы разберем далее.

Так называемая аксонометрия не имеет ничего общего с реальностью.
СОКРАЩЕНИЕ СТОРОН
Все эти упражнения помогут понять основные принципы перпективы, но они не учитывают всех её особенностей.
Каждая сторона, каждой оси находится на разном расстоянии от нас – зрителя. Что значит они просто не могут быть идентичной длинны, ширины или высоты. Так как согласно принципам перспективы чем дальше находится объект, тем он выглядит меньше и наоборот.


Тоже касается и сторон объекта – дальние стороны будут сокращаться в размерах, а значит и сами стороны по мере отдаления будут сужаться.

Тоже касается и незначительного сужения нижних сторон, так как они тоже находятся чуть ниже, а значит дальше от нас – зрителя.

Эти явления вы могли замечать, глядя на разные объекты, такие как здания, дороги и машины, на их дальние стороны, и сравнивая насколько меньше они кажутся по мере отдаления от нас.

Более подробно эту тему разбирает Урок №8 Линейная перспектива.
ЛИНИЯ ГОРИЗОНТА И УРОВЕНЬ ГЛАЗ
Любой объект, когда мы на него смотрим, находится либо под нами, либо над нами, либо прямо перед нами. А также он может находится от нас по правую сторону либо по левую. Всё это влияет на трехмерный вид объекта в перспективе, то каким мы его видим.

Одим из таких факторов является линия горизонта, она определяет будем мы видеть крышку объекта либо его дно, или ни то и ни другое (когда объект находится непосредственно перед нами, на линии горизонта).
При этом обратите внимание, чем дальше объект находится от линии горизонта, тем круче и острее выглядят его углы.








Попробуйте, шаг за шагом, нарисовать прямоугольники на разных расстояниях от линии горизонта, на виде спереди и в три четверти, как показано выше и ниже:






ЛИНИЯ ГОРИЗОНТА И ОКРУЖНОСТИ
Не смотря на то, что у окружности нет крышки и нет дна, линия горизонта всё равно определяет как мы будем её видеть.

Прежде всего это происходит также за счёт изменения градуса центральной оси объекта. Давайте рассмотрим это на примере ниже:
Шаг 1. Изобразим окружность и сопоставим двум предыдущим ракурсам прямоугольника. Таким образом окружность займёт некое среднее положение между видом спереди и три четверти.

Шаг 2. Отметим визуально лицевую сторону точкой, благодаря которой мы сможем наблюдать постепенный разворот окружности.

Шаг 3. Помимо центральной оси у каждого объекта всегда есть перпендикулярная ось, которая также делит объект пополам.

Шаг 4. Изобразим несколько таких осей вдоль окружности, чтобы также наблюдать за изменениями их кривой линии.

Шаг 5. Затем отметим ещё одну точку, теперь уже на перпендикулярной оси и проведём от неё линию до лицевой точки.
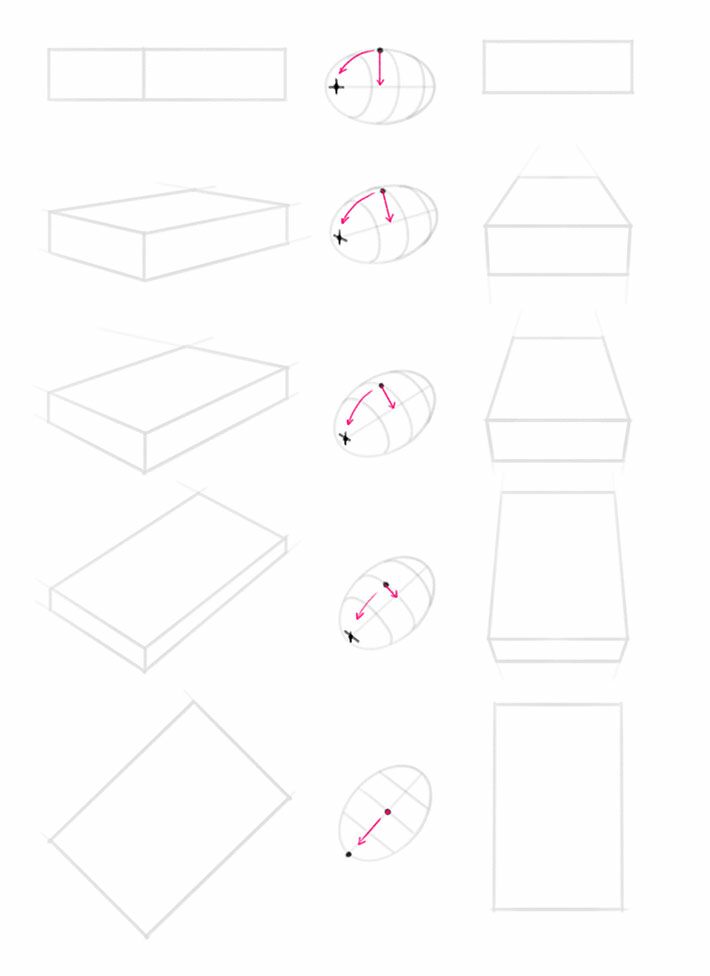
Шаг 6. Получился продольный разрез, смещение которого мы также можем наблюдать по мере отдаления окружности от линии горизонта.

Шаг 7. Отметим еще одну точку, но теперь обозначив боковую продольную линию.

Шаг 8. И также проведём от неё линию до лицевой точки.

Шаг 9. Готово, у нас получилась окружность - эллипсойд в перспективе.

Как видите по мере снижения эллиспойда ниже линии горизонта (уровня глаз), мы всё больше видим его верхушку.

Попробуйте ещё порисовать эллипсойды под разным углом, за счёт изменения градуса центральной оси объекта.

Конечно это не единственный способ построения окружности в перспективе и далее мы рассмотрим другие варианты.
ПЕРСПЕКТИВА ОКРУЖНОСТИ
Как мы уже говорили, перспективе подчиняются не только прямоугольники, но и овальные объекты такие как сферы цилиндры и эллипсы. Эти фигуры не имеют квадратных граней, зато все они имеют оси: ширины, высоты и глубины. Длина этих осей и углы между ними определяют вид и угол наклона трехмерной фигуры.

Давайте теперь разберем это на примере. Самый простой способ нарисовать эллипс - изобразить крест перпендикулярных осей, завершив их короткими отрезками на конце, а затем добавить отрезки между ними, как показано ниже. И в конце всё это обвести окружностью.

Эллипсы в объёме называют эллипсойдами, они состоят из трех продольных осей: сверху (1), сбоку (2) и спереди (3).

Части тела животного или человека имеют эллипсойдные или капсульные формы (голова, плечи, грудь и т.д.), как показано ниже:

Выглядит сложно, к счастью эллипсоид следует правилам ограничивающего прямоугольника. Мы уже умеем строить прямоугольники, так что давайте сразу перейдем к построению окружностей.
Более подробно перспективу окружности мы разберем в уроке №9
Шаг 1
Нарисуйте горизонтальный прямоугольник в перспективе, проведите диагонали на каждой стороне побокам и соедините их.

Шаг 2
Проведите такие же диагонали на каждой из сторон прямоугольника - так мы сможем точно определить положение осей окружностей.


Шаг 3
Получились оси с точками, которые касаются сторон ограничивающего прямоугольника.

Шаг 4
Проведите через эти точки линии сторон прямоугольников, в которые мы будем вписывать эллипсы.

Шаг 5
Проведите диагональные линии от углов прямоугольника.

Шаг 6
Теперь нарисуйте два коротких отрезка на концах центральной оси.

Шаг 7
Нарисуйте остальные отрезки: длинными для области тупого угла и короткими для острого угла.

Шаг 8
Теперь можете соединить эллипс. Противоположные дуги должны быть идентичны друг другу.


Шаг 9
Проделайте то же самое с другими прямоугольниками.

Шаг 10
Теперь вы можете нарисовать контур внешнего эллипса. Убедитесь, что все эллипсы заключены внутрь.

Можно скрыть невидимые стороны.

Вам не придётся каждый раз повторять весь этот процесс. С практикой вы научитесь рисовать эллипсоид на глаз.
ЭЛЛИПСОЙД НА ГЛАЗ
Предположим, вы хотите нарисовать эллипсойд сразу. Представьте какую бы форму он имел, какого размера и нарисуйте!

Теперь выделите переднюю, верхнюю и боковую часть эллипсойда.

Отметьте центральную точку с каждой стороны.

Проведите от каждой точки линии направления осей. Если вам сложно сделать это на глаз, вернитесь к предыдущим упражнениям, чтобы еще немного потренироваться.

Длина линий и углы между ними взяты условно!
Теперь нарисуйте плоскости окружности каждой из осей.

Наконец, нарисуйте эллиптический контур осей, как показано ниже.

Вот ускоренная версия процесса:

Нарисуйте разные виды капсул и эллипсойдов с разных ракурсов. Чем больше практики, тем лучше!

Как видите, построение эллипсойдов не сильно отличается от построения прямоугольников.

В обоих влучаях есть: стороны, угол наклона и ось направления.
ОРГАНИЧЕСКИЕ ФОРМЫ
Кажется что органические формы уклоняются от правил перспективы, так как у них нет прямых линий, но у них есть эллипсы, и угол наклона, и оси которые следуют определённым направлениям.

Давайте нарисуем змееобразные фигуры, но для начала нам понадобятся прямоугольные основания, чтобы было на что ориентироваться.
Шаг 1. Нарисуйте прямой вертикальный отрезок и две диагональные линии, расходящиеся в разные стороны. Затем добавьте нижнюю часть основания.


Отмерьте правый и левый конец, условной длинны и ширины. Соедините оба конца под тем же углом, что и первые диагональные линии.


Шаг 2. Нарисуйте три таких прямоугольных основания.

Шаг 3. На каждом основании изобразите ось направления (выделено красным цветом) и небольшую спираль, постепенно сокращая диаметр по мере отдаления.

Шаг 4. Теперь нам нужно отрисовать эллипсы ориентируясь по центральной оси направления каждой фигуры.

Шаг 5. В местах изгибов со внутренней стороны расстояние между эллипсами будет сокращаться, а с наружней стороны расширяться.

Шаг 6. Теперь можно добавить контуры.

Шаг 7. Можно также добавить центральные точки на лицевой стороне каждой фигуры и от них продолжить оси сечения. Готово!

Давайте построим ещё одну фигуру. Начнем с прямоугольного основания, затем нарисуем ось направления и небольшую спираль, постепенно сокращая диаметр по мере отдаления. Затем ориентируясь на поворот фигуры и прямоугольное основание, отрисуем все эллипсы шаг за шагом.


Например направление центрального эллипса совпадает с направлением основания. Некоторые эллипсы развёрнуты к нам боком, поэтому мы будем видеть их лишь в виде полосок.


Некоторые эллипсы почти параллельны передней стороне основания, поэтому они будут более размернуты к нам.
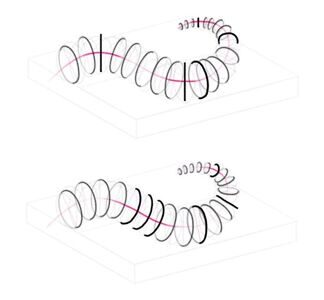

Как видите, в зависимости от того, как мы развернем эллипсы, получается разный разворот змейки. При этом линия направления и контур фигуры остаются прежними.

Получилась зрительная иллюзия, связанная с ракурсом эллипсов в перспективе.
ОСИ НАПРАВЛЕНИЯ ОБЪЕКТА
Как вы успели заметить, многое можно построить используя оси направления объектов. Особенно если дело касается живых существ в движении.
Более подробно мы разберем эту тему на следующем Уроке №6 - Думайте формами.
Шаг 1. Давайте нарисуем оси направления объектов с разными изгибами.

Шаг 2. Теперь давайте выберем для кадого изгиба разное сечение. Это может быть круг, ромб, прямоугольник и т.д.

Шаг 3. Сверху нарисуем спираль, постепенно сокращая диаметр по мере отдаления.
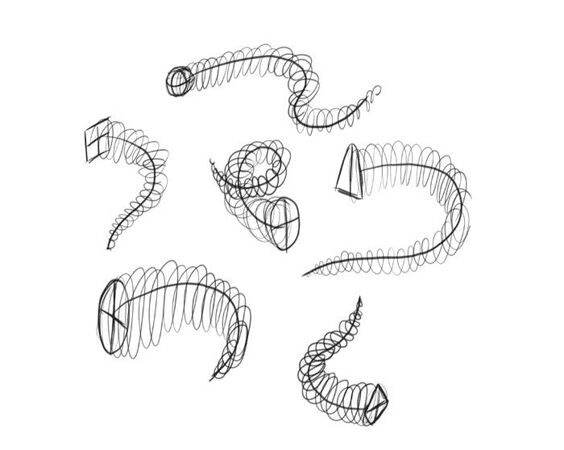
Шаг 4. Теперь проведем линию от центра вдоль их «позвоночника», представьте что это живые существа.

Шаг 5. Затем несколько раз повторите контур сечения вдоль оси направления, учитывая изгиб каждого объекта.

Шаг 6. Заполните все пробелы, чтобы не было пустых участков. С внутренней стороны изгибов контуры должны быть плотнее, а снаружи изгибов наоборот шире.

Шаг 7. Если вы хотите сделать фигуры более объемными, можно добавить светотень.

Как видите можно легко построить органическую форму используя ось направления и контуры сечения.
Более подробно рисование органических форм мы разберем в уроке №10
На сегодня это все! Эти упражнения не предназначены для выполнения в одночасье, но перспективу нельзя игнорировать - вы либо знаете, что делаете, либо гадаете. Это сложная тема, поэтому вы должны регулярно практиковаться. Чтобы полноценно изучить перспективу вам также будут полезны следующие уроки:
Курс рисования на графическом планшете. Урок №8 - Линейная перспектива
Курс рисования на графическом планшете. Урок №9 - Перспектива окружности
Получилась очень длинная статья, методический материал был взят с сайта: https://monikazagrobelna.com
На следующем уроке мы разберем способность думать и видеть формами.


Комментариев пока нет